Graph clustering: an approach based on "prominent vertexes"

I was doing some experiments on the entropy graph, and I noticed that under some conditions it is a good marker of special vertexes.
I'll try to explain the concept without formulas: that's really challenging because of my English :)
These vertexes play a special role that I decided (arbitrarily) to call "Prominent Vertexes": basically if you remove them, you introduce some disconnections on the graph; the remaining connected components are the clusters that induce the graph partitioning. To be more precise the connected components return just the N-1 clusters, the last cluster is obtained by the complement operation between the original graph and the N-1 clusters.

The intuitive explanation

• Consider all the possible paths between two nodes A and B in a graph
• Let's take for the above paths the intersection of them.
• The result is a set of nodes that are essential to connect the two nodes: these nodes are the prominent nodes for the vertexes A and B

The above schema can be applied (with some expedient) to all the Binomial[N,2] pairs of vertexes.

Some result

1st example

Let's consider the following graph and the respective "prominent vertexes":

In yellow have been depicted the prominent nodes for the graph

The clusters obtained considering the connected components are the following:

The 3 clusters obtained on the graph

As usual I compared my approach against another technique:  A. Clauset, "Finding Local Community Structure in Networks," Physical Review E, 72, 026132, 2005.

The 6 clusters obtained through the "Clauset" method.

Comment:

As you can see the proposed approach seems to be much less fragmented respect the Clauset method.

2nd example

Here is another example:

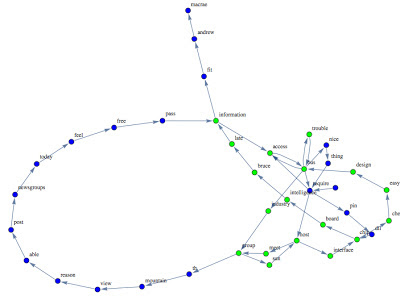The 2 clusters obtained with the prominent vertexes method,

The 6 clusters obtained through the Clauset method.

Comment:

As in the former example the "prominent vertexes" method seems to behave better (even if the result is not optimal).

Considerations

PRO

• The method proposed seems to be a promising graph clustering algorithm.
• The method doesn't require parameters (e.g. number of clusters).
• The method doesn't fragment to much the nodes. 

CONS

• The complexity is (for the current implementation) quite high ~Binomial[Graph Order, 2].
• The method requires improvements and theoretical explanation.
• The method has lower accuracy when the vertexes degree is very small.

The code will be released as soon as the formalization of the Entropy Graph is completed.

Looking forward to receive your comments.

Stay tuned & Merry Christmas!

c.