I have to clarify that:
- This method is just a consideration about the role played by some vertexes in a generic (directed) graph.
- The results posted in the former graph can be a lot improved (I'm working on it among the several streams that I opened around the concept of entropy graph!).
- the approach I'm going to explain in this post is not the same I used in the former because I prefer focus on the main idea respect the optimizations (but exential) aspects.
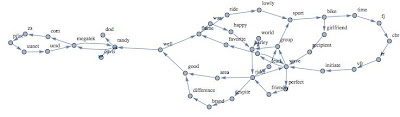
Let's consider the following graph:
Let's consider two nodes: "cbr" and "zx", then let's take all the paths that connect the two nodes:
 |
| All the possible paths between the node "cbr" and "zx" |
We have now to consider the intersection (excluding the starting and ending points) among the all paths:
such nodes are essential in order to reach the node "zx" from "cbr"because excluding just one of them, you cannot reach the ending point!
 |
| The prominent nodes for the pair ("cbr","zx"): |
In the above procedure we found out the prominent nodes related to the pair "cbr", "zx".
Of course in order to determine the prominent nodes of the entire graph you have to consider all the pairs of nodes: that's the reason that justify the complexity >Binomial [n,2] of the procedure (n = order of the graph). The complexity doesn't consider the complexity to obtain the paths between the nodes!
The final result can be obtained taking the intersection of all "prominent nodes" for each pairs of nodes!
As you can imagine this is an expensive way to obtain the prominent nodes: I'll provide you an update about improvement on it.
Stay tuned
cristian