Document as Stochastic Process: My contribute - part 1

Abstract
A statistical discrete distribution (based on geometric random variable) to depict a document. In the post it's presented a probabilistic density function to describe a document thru the underlying stochastic process.

PDF-CDF charts and  PDF analytical formula for document of length Z.

Results for a document of two words.

Introduction
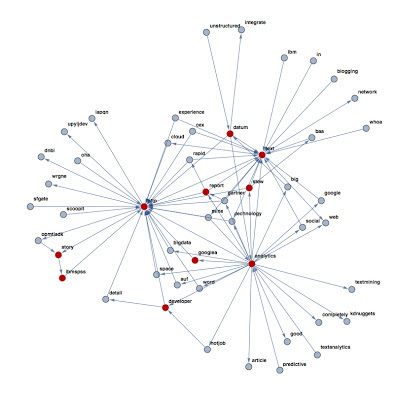
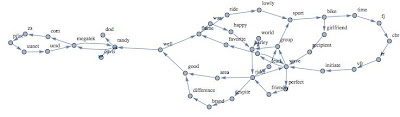
We often discussed about the importance of the features extraction step in order to represent a document.

So far, I mostly presented techniques based on "bag of words" and some more sophisticated approach to capture the relation among such features (the graph entropy, mutual information, and so on).

In the last weeks I started to think about a different perspective in order to capture the essence of a document.

The idea

What is a document from statistical point of view?

I tried to give an answer, and I came to the following (expected) conclusion:

1. A document is a stochastic process of random variables - the words of the document.
2. In a document as in a whatever statistic process, the occurrences of the random variables and functions over them doesn't provide complete description of the process.
3. The joint distribution of the waiting times between two occurrences of the same variable (word) encloses all the significative links among the words. 

The idea is to depict a document as stochastic process of "waiting time" random variables.

This formalization allows us to think to a document as a statistic distribution characterized by its own density and cumulate function.
The waiting time is very well depicted by geometric distribution.

Formalization 

A document is a process of geometrically distributed random variables:

N= size of the document, j = #words.

where each random variable is described as follow:

 Let's consider the following document composed by a sequence of two words: "a" and "b".

The Problem

• What is the probability function associated to a document Dk?

Given the following document:

The Probability of Dk is given by:

The below image should explain better what I meant:

Probability of Document Dk
q = 1-p

Probability Density Function 

-> From now, if not clearly specified I will refer to a document of two words (as above described).

Questions:

1. What is the analytical representation of the above function?
2. Is it the above function a probability function?

1. Analytical formulation

This is the funny part: I like combinatoric... the art of tally!

To solve the problem, I'm sure, there are several strategies, I used just the way that is more aligned to my mind setting: I put all the options on the table and I start to check to gather them together  according to some criteria :)

• The formulation of the "p" is a joke: the sum of the exponents must be equal to the size of the vector.
• the formulation for the "q" requires some deeper thinking.

As you know, I don't like too much technicalities, so I spare you the theoretical aspects.
I think it's more worthwhile  to show how the solution comes!

Exponents:
Let's put the q_a and q_b  exponents properly sorted on a matrix:

The split over the anti-diagonal makes the calculus easier.

Coefficients:

 The same configuration of exponents can be related to different configurations of the words in the document:

The different configurations (20) of two words in a document having length = 8. 

 Let's put the the occurrences of the different configurations of words for the same exponents configuration in a matrix:

# occurrences of the different configurations of words for the same exponents configuration.

Do you see the similarities respect the two halves of the matrix?

Is it easier now find the "low" to build the above matrix?

... If you don't like play around with combinatorics, you can ask help to  The On-Line Encyclopedia of Integer Sequences®!

Ok, ok you are too lazy...: the solution is Binomial[k+i,k].

The Analytical formula

The above matrixes suggest that the analytical formula is composed by two main addends: one for the orange side and another one for the green side.
For a document of two words the Probability Density Function is the following:

PDF for a document composed by two words.
qa = 1-pa = pb; pa+pb = 1.

I don't want enter in theoretical details to proof that the above formula is probability function (after all this is a blog by practical means!).
The only point I want to remark is that the convergence to a PDF is guaranteed for a length of document that tends to Infinity.
The above formula can be further reduced and simplified (in the easy case of 2 words) if you consider the following conditions:

qa = 1-pa = pb => qb=pa (pa+pb = 1).

Basically in the above case the PDF is function of 1 variable.

PDF and CDF for a document of 2 words.

In the CDF, we sum the probability contribute of all documents composed by two words having length =1, 2, ..., Infinity.
As you can see, the contribute of documents having length >50 is negligible for whatever value of pa.

These kind of distributions based on geometric variables are often used in maintenance and reliability problems, so I encourage you to have some reading on that!


Next Steps
In the next posts I'm going to explain

• some properties of the function
• its extension to multiple variables  
• entropy
• practical applications 

Last Consideration
I did the above exercise just for fun, with out any pretension to have discovered something new and or original: if you have some paper/book/reference about identical or similar work, please don't hesitate to contact me!

Don't rush, stay tuned
cristian

Image objects recognition: a basic approach

To complete the brief dissertation on the most popular problems of the image analysis science, I did a couple of experiments on a very intriguing topic: the identification of specific objects within an image.
I didn't use "state of art" algorithms (...my knowledge on the field is not deep and I wont use techniques that I don't fully understand!).
The target of this experiment isn't to show the best way, but just to show the rudiments of the matter.

Objective
Given an image called target image, and given another image called feature, the objective is to identify the features within the target image.

Technique 
I decided to play with a technique that I studied on signal processing course at University: the matrix correlation.

The matrix correlation is typically used to detect similarities between two 2D signals, which are often saved in matrices. 

The magnitude of the correlation shows how similar the signals are. If the correlation is large, the two signals are considered to be very similar. Alternatively, if correlation is zero, the two signals are considered to be independent. Analytical definition and explanation are available in all books of signal processing.

Experiment: Ball detection

In the first example I will try to detect the balls in the target image:

On the left the target image. On the right the feature (the ball!) to be identified in the image.

To solve the problem, I tried to apply the algorithm directly to the original images, but the results were terrible, so I applied some image manipulation technique in order to make more digestible the input to the main algorithm: I never be tired to say that preprocessing is crucial to solve a problem!

The algorithms used here are: edge detection and binarization. So I feed the correlation algorithm with the following input:

The input used to feed the correlation algorithm obtained with Binarization and eEge Detection techniques.

Results

Finally we can show the output: we can check if the algorithm identified correctly in the target image the balls!

To highlight the results I played around with colors and image merging :)

Results: balls identified in the image 

 As you can see the results are not so bad, and playing around with a preprocessing parameters I'm sure it's possible to improve the accuracy.

Experiment: Painting Recognition

I Applied the same technique to identify the paintings hung on a wall:

Target image: paintings hung on a wall

Results:

The techniques used are same of the above experiment, so let's go directly to the results:

Paintings detected

Considerations

The technique is quite rough and the accuracy depends on 

• Preprocessing technique applied 
• Measure used to compute the correlation (in both experiment I used cosine distance)

The algorithm per se seems to be not so general purpose to be used for such objective, but it's a good  starting point to approach the problem. Maybe if the feature to be detected is always the same (for instance as in face recognition), the accuracy is acceptable.

Stay Tuned

Cristian

Image comparison: SURF algorithm

In the former post I showed a naif approach that can be easily implemented and that works quite well under the condition that the image is not subjected to distortions.
I decided to deepen a bit the topic just for the sake of the curiosity ( curiosity and imagination are the skills that I most appreciate at work!).

SURF stands for "Speeded Up Robust Features" and it has been published by Herbert Bay, Andreas Ess, Tinne Tuytelaars, Luc Van Gool in 2008. The original paper is available here.

I strongly recommend to read the paper: it's self contained and it's very clear to be read also by neophyte  as I.
As usual I go straight to the experiments and to discuss the results.

Experiment
I considered again the same data set of the last post, and I tried to compare all the possible combinations  of pairs of images  to check the accuracy of the algorithm.

The first step of the algorithm is to determine the key features of an image.

key features detection

Once the features have been detected it's possible to use them for the comparison through euclidean measures or similar.

In the below image I plotted the common points and their position between two images:

Common points found between two images. In yellow I depicted them and their position.

If you zoom a bit the image you will notice that the common points found are thousands. To find them the algorithm took around four minutes.

In a productive environment this amount of time could be not acceptable. 

To improve the situation and reduce the computational time, I processed the image with binarization filters; after this preprocessing the time has been reduced from 4 minutes to 25 seconds.

Results

In the below matrix I listed all the comparison done to check the accuracy.

The correct pairs lay on the principal diagonal of the matrix.

In red have been listed the correct pairs

To show graphically the results I plotted over the matrix the number of common points found for each pair. The colors chosen highlight that number. 

Conclusions

As you can see for all the pairs on the principal diagonal the algorithm detected the highest number of common points.

In the next post I will show how to use this algorithm to identify logos in a document.

Stay tuned

Cristian

Image comparison for dummies: an easy and fast approach

Since I started to blog, I presented different methods, techniques and tricks to solve problems related to Data mining, and text mining (... I'm still puzzled about the difference between text mining and text analytics). 

Today I would like to present a different approach to solve a common problem in the text analytics area: the document comparison problem.

The problem
Usually if you want to compare two documents in order to check if they are pretty much the same you can apply some easy tricks in order to check frequency and position of the words.
Sometime the documents  require an OCR processing in order to get the "text rendition" for the documents, and such process usually is a very expensive in term of computational time (often it takes more than 10 seconds per page): what if you have to perform many comparison checks and you are short in time?
...In that case I suggest to consider the documents as images!

Image processing approach
This branch of the computer science evolved quite fast in the last decade and it achieves a level of complexity extremely high.
I'm not an expert at all, and many libraries (often free as opencv) are available and they offer several functionalities: image comparison, image recognition and so on.
Unfortunately I'm stubborn and curious and I like try to do experiments :).

So I decided to implement a very easy algorithm able to compare with high accuracy documents very similar.

Algorithm:
1. Resize the image (in order to have images having the same number of pixels)
2. Binarize the image
3. compute the histogram distribution
4. perform the comparison considering the Kullback distance between the two empirical distributions got from the histograms.

Considerations:

•  such algorithm is not robust to linear transformation/distortions of the image (but this is not case when you compare documents...).
• it's very fast respect the solutions that require OCR processing.
• it could be easily optimized considering sub-block of the images (and give higher weights to blocks in the middle of the image).
• through some assumptions based on eigenvectors it could be helpful also in case of image linear transformations.

Experiment

I selected 10 random images (pictures, medical analysis, text, screenshot):

Original sample set 

   

For each document, after some image adjust filter, I computed the histograms:

Histograms for the above images

I introduced some noise in each of the documents and I computed again the histograms:

Noised sample set.

Histograms for the noised images

As you can see, despite the noise introduced is quite big, the characteristic histogram seems to preserve quite well the shape.

Results:

I compared each possible possible combination of the pairs composed by original image and noised image and I ranked the result of the comparison.

...The test has been passed with an accuracy of 100%.

I have to say that the images are quite heterogeneous among each other, but further tests (I'll publish them in one of the next posts) highlighted that the method is quite robust (with all the limitations explained above).

Here is some of the best matching found:

Some of the best matching found

...I have to say that the image processing is a very fascinating  science!
Stay tuned
cristian

Mind maps of #textanalytics - automatic generation

What I want to show you today is "snippet" of a project I'm working during my spare time.
The project has the aim to gather, provide and represent the knowledge in a different way.
For the time being I don't want to disclose too much info, but the main idea is to leverage my concept of the graph entropy to capture information in a document (or in a data set) to create a new kind of indexer.

One of the output of the algorithm is the generation of the mind map.

Experiment
Through the API provided by Twitter I downloaded the last 200 tweets from the hashtag #textanalytics.
I processed the tweets and here is the results:

#textanalytics mind map

In red have been depicted the first 10 relevant words extracted through the graph entropy criteria.
It's interesting notice how the map shows intuitively the links among the words.
Of course the map can be enriched with more links or more relevant words: the choice depends on the user choice.
In the next posts I'll show you how the clustering techniques discussed in the former posts can be profitably used to create homogeneous group of words related each others.
what do you think?
Stay  tuned
cristian

Graph Clustering through "prominent vertexes": some clarification

I received many mails about the last post, and most of them asking explanations about the technique I developed.
I have to clarify that:

1. This method is just a consideration about the role played by some vertexes in a generic (directed) graph.
2. The results posted in the former graph can be a lot improved (I'm working on it among the several streams that I opened around the concept of entropy graph!).
3. the approach I'm going to explain in this post is not the same I used in the former because I prefer focus on the main idea respect the optimizations (but exential) aspects.

Let's consider the following graph:

Let's consider two nodes: "cbr" and "zx", then let's take all the paths that connect the two nodes:

All the possible paths between the node "cbr" and "zx"

We have now to consider the intersection (excluding the starting and ending points) among the all paths: 

such nodes are essential in order to reach the node "zx" from "cbr"because excluding just one of them, you cannot reach the ending point! 

The prominent nodes for the pair ("cbr","zx"): 

In the above procedure we found out the prominent nodes related to the pair "cbr", "zx".

Of course in order to determine the prominent nodes of the entire graph you have to consider all the pairs of nodes: that's the reason that justify the complexity >Binomial [n,2] of the procedure (n = order of the graph). The complexity doesn't consider the complexity to obtain the paths between the nodes!

The final result can be obtained taking the intersection of all "prominent nodes" for each pairs of nodes!

As you can imagine this is an expensive way to obtain the prominent nodes: I'll provide you an update about improvement on it.

Stay tuned 

cristian