Support Vector Regression (SVR): predict earthquakes through sunspots

In the last months we discussed a lot about text mining algorithms, I would like for a while focus on data mining aspects.
Today I would talk about one of the most intriguing topics related to data mining tasks: the regression  analysis.
As you know the regression analysis is an approach to modeling the relationship between a set of variables "y" and  explanatory variables "x" (called regressor).
The model I've chosen to talk about regression is strictly related to the SVM algorithm already presented in our classification problems: Support Vector Regression (SVR).


How does it work?
In SVR the basic idea is to map the data x into a high-dimensional feature space F via a nonlinear mapping  and to do linear regression in this space.


Why SVR?

• SVR is extremely robust even in input space having high dimension because the optimization doesn't depend on the dimension of input space.
• SVR depends only on a subset of the training data, because the cost function for building the model ignores any training data close to the model prediction.
• SVR over ordinary linear regression has the advantage  of using a large variety of loss functions to suit different noise models.
• SVR is more robust than linear regression for noise distributions close to uniform.

I don't want spend words about the theory, there are several tutorials on it downloadable from scholar google.

Applications

The regression models are widely used to infer a phenomena through several variables. Financial forecasting, risk management, clinical tests,  are just examples of areas where these techniques are applied.

Consider for instance earthquake events: imagine for an insurance company how can be relevant assign a risk score to define the right premium for such risk.

For this kind of market a predictor based on other variables already available or at least on variables easier to predict could represent a solid base to assess the right price for the premium and, the discovery of new predictors could represent a huge advantage respect competitors.

...Let's try to play with SVR:

Experiment: Earthquakes prediction using sunspots as regressor

Early warning: this is just a tutorial, so don't consider the results of this experiment as a real scientific work on earthquake prediction!

Data considered:

- series of earthquakes registered in USA since 1774 to 1989.

- series of sunspots registered since 1774 to 1989.

Let's plot the graph of the number of quakes registered per year and the related number of sunspot:

The two coplanar axis are respectively the "time line" and "# sunspots", the z axis represents the number of earthquake registered.    

As you can see the graph shows a significant increasing of the number of earthquakes registered when the number of sunspots are dramatically low and high.

What about the magnitude? 

The two coplanar axis are respectively the "time line" and "# sunspots", the z axis represents the highest magnitude of earthquakes registered. 

The above graph returns exactly the same information: to low number of sunspots or high number of sunspots corresponds to higher magnitude of earthquakes.

Support Vector Regression

I removed the time line axis; the below graph shows the number of earthquakes and the respective number of sunspots:

On X axis # sunspots, on Y axis # earthquakes.
(the point have been joined just for the sake of clarity)

I played a bit with Gaussian kernels, and here you are the results of the SVR regression:

In Red the original data, in Blue the predicted data. 

As you can see the model is extremely precise especially when the sunspots are greater than 50.

For low values of # sunspots the predictor tends to underestimate the number of earthquakes occurred.

Same considerations in prediction of magnitude:

We will see how to improve the accuracy.

Stay tuned!

cristian 

Appendix

Sunspot series:

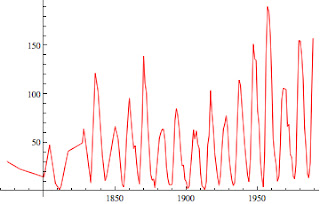Sunspots series

Earthquake series:

Earthquake series.
... The increasing of number of quakes is suspicious.  

The regressor found: